- Das 1. Keplersche Gesetz
-
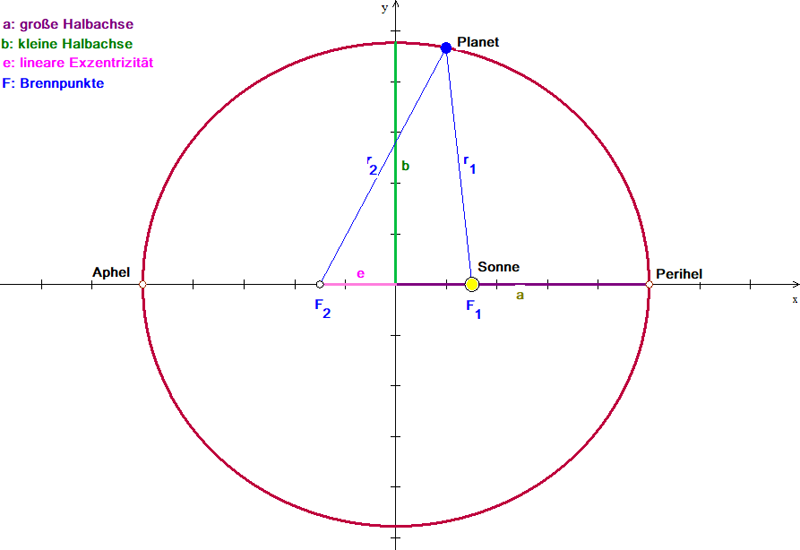
Die Umlaufbahnen der Planeten um die Sonne sind Ellipsen
mit der Sonne in einem der beiden Brennpunkte.
-
Eine Ellipse ist dadurch gekennzeichnet, dass in jedem Bahnpunkt die Summe der Abstände
von den beiden Brennpunkten konstant ist:
\(r_1 + r_2 = 2a = const\)
Der sonnenfernste Bahnpunkt heißt Aphel, der sonnennächste Punkt Perihel.
Die numerische Exzentrizität \(\varepsilon\) gibt an, welchen Bruchteil der großen Halbachse die lineare Exzentrizität \(e\) ausmacht:
\(e = \varepsilon\cdot a\) mit \(0 \le \varepsilon \le 1\)
Für die kleine Halbachse gilt:
\(b^2 = a^2 - e^2 = a^2(1-\varepsilon^2)\)
In der folgenden Animation wird \(\varepsilon\) von \(0\) bis \(1\) und wieder zurück verändert. Man erkennt:
Bei \(\varepsilon=0\) ist \(b=a\), die Brennpunkte fallen im Mittelpunkt zusammen, und die Ellipse wird zum Kreis mit Radius \(r=a\).
Für \(\varepsilon=1\) entartet die Ellipse zu einer Strecke.Für die Erdbahnellipse gilt \(\varepsilon=0,0167\), das heißt, sie unterscheidet sich nur sehr geringfügig von einer Kreisbahn. Das Endbild der Animation kommt dieser Tatsache sehr nahe.
- Das 2. Keplersche Gesetz
-
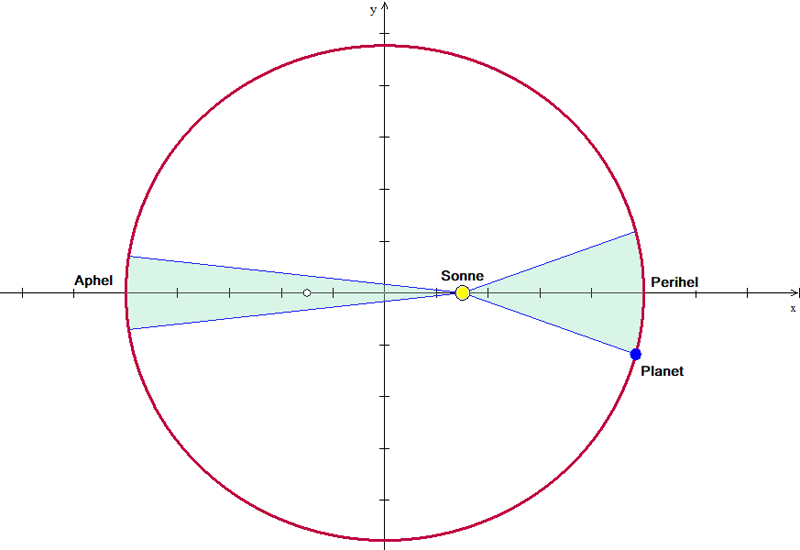
Die gedachte Verbindungslinie Sonne – Planet überstreicht
in gleich langen Zeitabschnitten gleich große Flächen.
-
Die beiden getönten Flächen sind inhaltsgleich, d. h. der rechte Bahnbogen ist länger als der linke. Da der Planet für beide Bögen die gleiche Zeit benötigt, muss seine Bahngeschwindigkeit rechts größer sein als links. Daraus folgt:
Der Planet bewegt sich in Sonnennähe schneller als in Sonnenferne.
- Das 3. Keplersche Gesetz
- Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die dritten Potenzen ihrer großen Halbachsen:
- \(\displaystyle\frac{T_1^2}{T_2^2} = \frac{a_1^3}{a_2^3} \)
-
Dieses Gesetz lässt sich an Hand der Planetendaten belegen. Als Referenz wählen wir die Erdbahn:
\(a_0 = 149,6\cdot 10^6\ \mbox{km = 1 AE }\)
(1 AE : Astronomische Einheit)
\(T_0 = 365,25\ \mbox{Tage = 1 Jahr}\)
Man erhält dann die folgende, auf die Erdbahn bezogene Tabelle der übrigen Planeten.
-
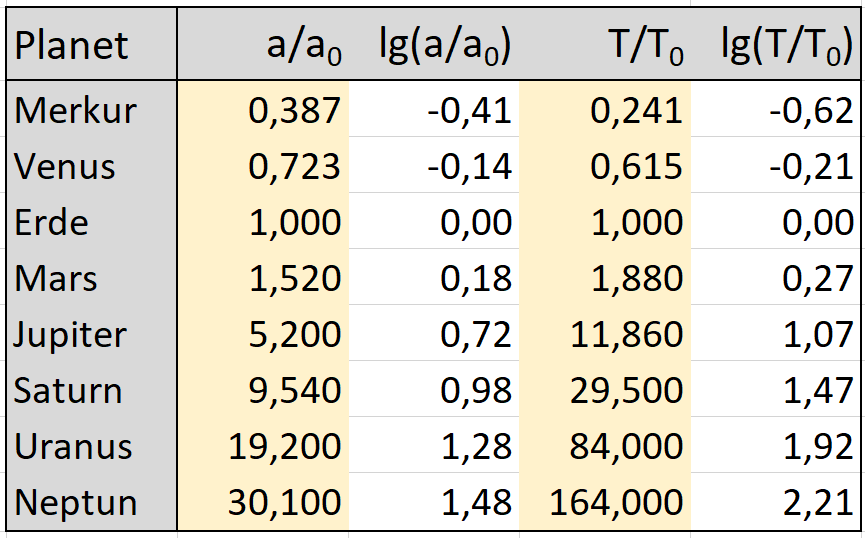
Trägt man die Logarithmenwerte in ein Koordinatensystem ein, ergibt sich folgender Graph:
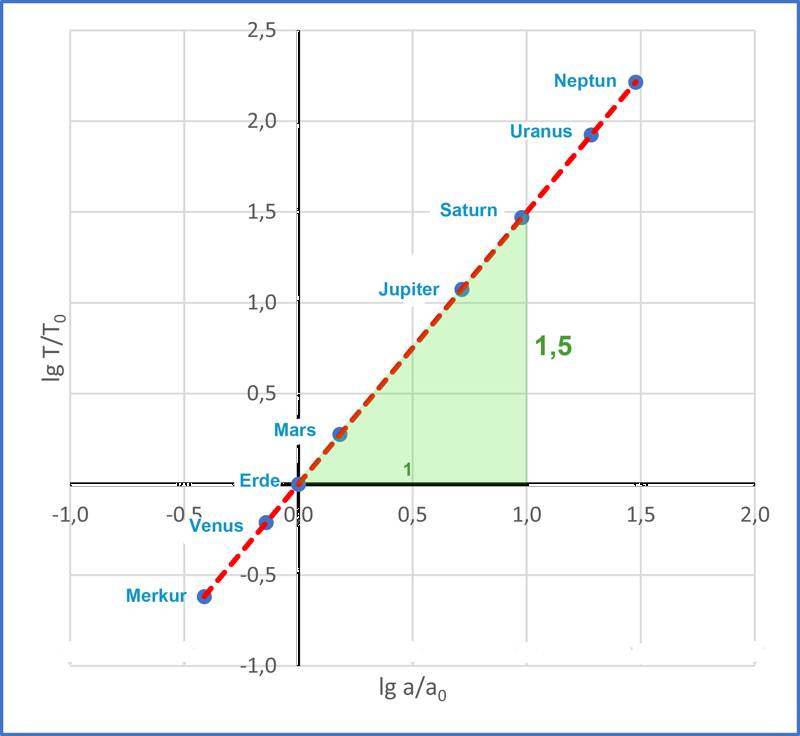
Wie man sieht, liegen die Messpunkte sehr gut auf einer Ursprungsgeraden mit der Steigung \(1,5=\frac{3}{2}\) (grünes Steigungsdreieck). Darauf folgt:
- \(\displaystyle\lg\frac{T}{T_0} = \frac{3}{2}\cdot\lg\frac{a}{a_0} \) oder \(\displaystyle 2\cdot\lg\frac{T}{T_0} = 3\cdot\lg\frac{a}{a_0} \)
Der Rest ist Algebra:
- \(\displaystyle\lg\left(\frac{T}{T_0}\right)^2 = \lg\left(\frac{a}{a_0}\right)^3 \) oder \(\displaystyle \left(\frac{T}{T_0}\right)^2 = \left(\frac{a}{a_0}\right)^3\)
Daraus folgt die Behauptung.
Die Keplerschen Gesetze